Contact forces, such as between a baseball and a bat, are explained on the small scale by the interaction of the charges in atoms and molecules in close proximity. They interact through forces that include the Coulomb force. Action at a distance is a force between objects that are not close enough for their atoms to “touch.” That is, they are separated by more than a few atomic diameters.
For example, a charged rubber comb attracts neutral bits of paper from a distance via the Coulomb force. It is very useful to think of an object being surrounded in space by a force field. The force field carries the force to another object (called a test object) some distance away.
CONCEPT OF A FIELD
A field is a way of conceptualizing and mapping the force that surrounds any object and acts on another object at a distance without apparent physical connection. For example, the gravitational field surrounding the earth (and all other masses) represents the gravitational force that would be experienced if another mass were placed at a given point within the field.
In the same way, the Coulomb force field surrounding any charge extends throughout space. Using Coulomb's law, \(F = k | q_{1}q_{2}|/r^2\), its magnitude is given by the equation \(F = k | qQ| /r^2\), for a point charge (a particle having a charge \(Q\)) acting on a test charge \(q\) at a distance \(r\) (see Figure 1). Both the magnitude and direction of the Coulomb force field depend on \(Q\) and the test charge \(q\).
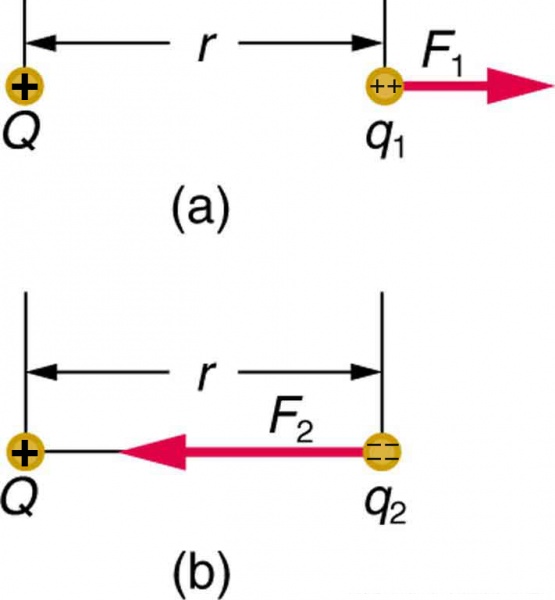
Figure 1The Coulomb force field due to a positive charge \(Q\) is shown acting on two different charges. Both charges are the same distance from \(Q\) . (a) Since \(q_{1}\) is positive, the force \(F_{1}\) acting on it is repulsive. (b) The charge \(q_{2}\) is negative and greater in magnitude than \(q_{1}\) , and so the force \(F_{2}\) acting on it is attractive and stronger than \(F_{1}\) . The Coulomb force field is thus not unique at any point in space, because it depends on the test charges \(q_{1}\) and \(q_{2}\) as well as the charge \(Q\).
To simplify things, we would prefer to have a field that depends only on \(Q\) and not on the test charge \(q\). The electric field is defined in such a manner that it represents only the charge creating it and is unique at every point in space. Specifically, the electric field \(E\) is defined to be the ratio of the Coulomb force to the test charge:
\(\mathbf{E} = \frac{\mathrm{F}}{q},\)
where \(\mathbf{F}\) is the electrostatic force (or Coulomb force) exerted on a positive test charge \(q\). It is understood that \(\mathbf{E}\) is in the same direction as \(\mathbf{F}\). It is also assumed that \(q\) is so small that it does not alter the charge distribution creating the electric field. The units of electric field are newtons per coulomb (N/C). If the electric field is known, then the electrostatic force on any charge \(q\) is simply obtained by multiplying charge times electric field, or \(\mathbf{F} = q \mathbf{E}\). Consider the electric field due to a point charge \(Q\). According to Coulomb's law, the force it exerts on a test charge \(q\) is \(F = k | qQ|/r^2\). Thus the magnitude of the electric field, \(E\), for a point charge is
\(E = \left | \frac{F}{q} \right | = k \left | \frac{qQ}{qr^2} \right | = k \frac{|Q|}{r^2}.\)
Since the test charge cancels, we see that
\(E = k \frac{|Q|}{r^2}.\)
The electric field is thus seen to depend only on the charge \(Q\) and the distance \(r\); it is completely independent of the test charge \(q\).
Calculate the strength and direction of the electric field E due to a point charge of 2.00 nC (nano-Coulombs) at a distance of 5.00 mm from the charge.
Strategy
We can find the electric field created by a point charge by using the equation \(E = kQ/r^2.\).
Solution
Here \(Q = 2.00 \times 10^{-9} \mathsf{C}\) and \(r = 5.00 \times 10^{-3} \mathrm{m}\). Entering those values into the above equation gives
\(E =k \frac{Q}{r^2}\)
\(= (8.99 \times 10^9 \thinspace \mathrm{N \cdot m^2/C^2}) \times \frac{(2.00 \times 10^{-9} \mathrm{C})}{ (5.00 \times 10^{-3} \thinspace \mathrm{m})^2}\)
\(= 7.19 \times 10^5 \thinspace \mathrm{N/C}.\)
Discussion
This electric field strength is the same at any point 5.00 mm away from the charge \(Q\) that creates the field. It is positive, meaning that it has a direction pointing away from the charge \(Q\).
What force does the electric field found in the previous example exert on a point charge of \(-0.250 \thinspace \mu \mathrm{C}\)?
Strategy
Since we know the electric field strength and the charge in the field, the force on that charge can be calculated using the definition of electric field \(\mathbf{E} = \mathbf{F}/q\) rearranged to \(\mathbf{E} = q \mathbf{E}.\).
Solution
The magnitude of the force on a charge \(q = -0.250 \thinspace \mu \mathrm{C}\) exerted by a field of strength \(E = 7.20 \times 10^5\) N/C is thus,
\(F = -qE\)
\(= (0.250 \times 10^{-6} \thinspace \mathrm{C})(7.20 \times 10^{5} \thinspace \mathrm{N/C})\)
\(=0.180 \thinspace \mathrm{N}.\)
Because \(q\) is negative, the force is directed opposite to the direction of the field.
Discussion
The force is attractive, as expected for unlike charges. (The field was created by a positive charge and here acts on a negative charge.) The charges in this example are typical of common static electricity, and the modest attractive force obtained is similar to forces experienced in static cling and similar situations.