Find the currents flowing in the circuit in Figure 5.
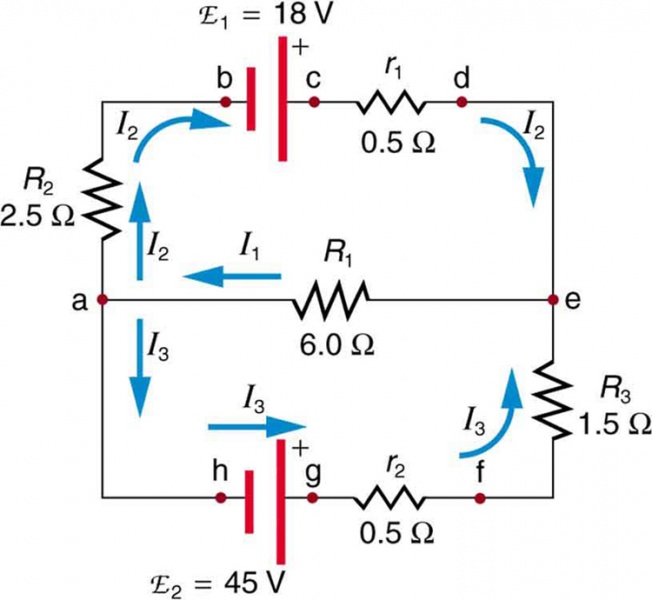
Figure 5. This circuit is similar to that in Figure 1, but the resistances and emfs are specified. (Each emf is denoted by script E.) The currents in each branch are labeled and assumed to move in the directions shown. This example uses Kirchhoff’s rules to find the currents.
Strategy
This circuit is sufficiently complex that the currents cannot be found using Ohm’s law and the series-parallel techniques—it is necessary to use Kirchhoff’s rules. Currents have been labeled \(I_{1},I_{2}\) and \(I_{3}\) in the figure and assumptions have been made about their directions. Locations on the diagram have been labeled with letters a through h. In the solution we will apply the junction and loop rules, seeking three independent equations to allow us to solve for the three unknown currents.
Solution
We begin by applying Kirchhoff’s first or junction rule at point a. This gives
\(I_{1} = I_{2} + I_{3}\)
since \(I_{1}\) flows into the junction, while \(I_{2}\) and \(I_{3}\) flow out. Applying the junction rule at e produces exactly the same equation, so that no new information is obtained. This is a single equation with three unknowns—three independent equations are needed, and so the loop rule must be applied.
Now we consider the loop abcdea. Going from a to b, we traverse \(R_{2}\) in the same (assumed) direction of the current \(I_{2}\), and so the change in potential is \(-I_{2}R_{2}\). Then going from b to c, we go from \(-\) to +, so that the change in potential is \(+\mathrm{emf_{1}}\). Traversing the internal resistance \(r_{1}\) from c to d gives \(-I_{2}r_{1}\). Completing the loop by going from d to a again traverses a resistor in the same direction as its current, giving a change in potential of \(-I_{1}R_{1}\).
The loop rule states that the changes in potential sum to zero. Thus,
\(-I_{2}R_{2} + \mathrm{emf_{1}} - I_{2}r_{1} - I_{1}R_{1} = -I_{2}(R_{2} + r_{1}) +\mathrm{emf_{1}} - I_{1}R_{1}=0.\)
Substituting values from the circuit diagram for the resistances and emf, and canceling the ampere unit gives
\(-3I_{2} + 18-6I_{1} = 0.\)
Now applying the loop rule to aefgha (we could have chosen abcdefgha as well) similarly gives
\(+I_{1}R_{1} + I_{3}R_{3}+I_{3}r_{2}- \mathrm{emf_{2}} = + I_{1}R_{1}+I_{3} (R_{3} +r_{2}) - \mathrm{emf_{2}} = 0.\)
Note that the signs are reversed compared with the other loop, because elements are traversed in the opposite direction. With values entered, this becomes
\(+ 6I_{1} + 2I_{3}-45 = 0.\)
These three equations are sufficient to solve for the three unknown currents. First, solve the second equation for \(I_{2}\):
Now solve the third equation for \(I_{3}\):
Substituting these two new equations into the first one allows us to find a value for \(I_{1}\):
\(I_{1}=I_{2}+I_{3} = (6-2I_{1}) + (22.5 - 3I_{1}) = 28.5 -5 I_{1}.\)
Combining terms gives
\(6I_{1} = 28.5 ,\) and
\(I_{1} = 4.75 \thinspace \mathrm{A}.\)
Substituting this value for \(I_{1}\) back into the fourth equation gives
\(I_{2}= 6 -2I_{1} = 6-9.50\)
\(I_{2} =3.50 \thinspace \mathrm{A}.\)
The minus sign means \(I_{2}\) flows in the direction opposite to that assumed in Figure 5.
Finally, substituting the value for \(I_{1}\) into the fifth equation gives
\(I_{3} = 22.5 - 3I_{1} = 22.5 - 14.25\)
\(I_{3} = 8.25 \thinspace \mathrm{A}.\)
Discussion
Just as a check, we note that indeed \(I_{1} = I_{2}+I_{3}\). The results could also have been checked by entering all of the values into the equation for the abcdefgha loop.
PROBLEM-SOLVING STRATEGIES FOR KIRCHHOFF'S RULES