Figure 5 shows the resistors from the previous two examples wired in a different way—a combination of series and parallel. We can consider \(R_{1}\) to be the resistance of wires leading to \(R_{1}\) and \(R_{3}\). (a) Find the total resistance. (b) What is the \(IR\) drop in \(R_{1}\)? (c) Find the current \(I_{2}\) through \(R_{2}\). (d) What power is dissipated by \(R_{2}\)?
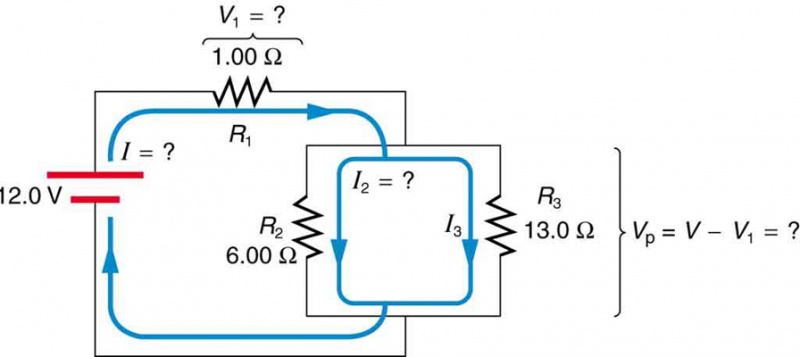
Figure 5. These three resistors are connected to a voltage source so that \(R_{2}\) and \(R_{3}\) are in parallel with one another and that combination is in series with \(R_{1}\).
Strategy and Solution for (a)
To find the total resistance, we note that \(R_{2}\) and \(R_{3}\) are in parallel and their combination \(R_{\mathrm{p}}\) is in series with \(R_{1}\). Thus the total (equivalent) resistance of this combination is
\(R_{\mathrm{tot}} = R_{1} + R_{\mathrm{p}}.\)
First, we find \(R_{\mathrm{p}}\) using the equation for resistors in parallel and entering known values:
\(\frac{1}{R_{\mathrm{p}}} = \frac{1}{R_{2}} + \frac{1}{R_{3}} = \frac{1}{6.00 \thinspace \Omega} + \frac{1}{13.0 \thinspace \Omega} = \frac{0.2436}{ \thinspace \Omega}.\)
Inverting gives
\(R_{\mathrm{p}} = \frac{1}{ 0.2436} \Omega = 4.11 \thinspace \Omega.\)
So the total resistance is
\(R_{\mathrm{tot}} = R_{1}+ R_{\mathrm{p}} = 1.00 \thinspace \Omega + 4.11 \thinspace \Omega = 5.11 \thinspace \Omega.\)
Discussion for (a)
The total resistance of this combination is intermediate between the pure series and pure parallel values (20.0 Ω and 0.804 Ω, respectively) found for the same resistors in the two previous examples.
Strategy and Solution for (b)
To find the \(IR\) drop in\(R_{1}\), we note that the full current \(I\) flows through \(R_{1}\). Thus its \(IR\) drop is
We must find \(I\) before we can calculate \(V_{1}\). The total current \(I\) is found using Ohm’s law for the circuit. That is,
\(I = \frac{V}{R_{\mathrm{tot}}} = \frac{12.0 \thinspace \mathrm{V}}{ 5.11 \thinspace \Omega} = 2.35 \thinspace \mathrm{A}.\)
Entering this into the expression above, we get
\(V_{1} = IR_{1} = (2.35 \thinspace \mathrm{A})(1.00 \thinspace \Omega) = 2.35 \thinspace \mathrm{V}.\)
Discussion for (b)
The voltage applied to \(R_{2}\) and \(R_{3}\) is less than the total voltage by an amount \(V_{1}\). When wire resistance is large, it can significantly affect the operation of the devices represented by \(R_{2}\) and \(R_{3}\).
Strategy and Solution for (c)
To find the current through \(R_{2}\), we must first find the voltage applied to it. We call this voltage \(V_{\mathrm{p}}\), because it is applied to a parallel combination of resistors. The voltage applied to both \(R_{2}\) and \(R_{3}\) is reduced by the amount \(V_{1}\), and so it is
\(V_{\mathrm{p}} = V- V_{1} = 12.0 \thinspace \mathrm{V} - 2.35 \thinspace\mathrm{V} = 9.65 \thinspace \mathrm{V}.\)
Now the current \(I_{2}\) through resistance \(R_{2}\) is found using Ohm’s law:
\(I_{2} = \frac{V_{\mathrm{p}}}{ R_{2}} = \frac{9.65 \thinspace \mathrm{V}}{ 6.00 \thinspace \Omega} = 1.61 \thinspace \mathrm{A}.\)
Discussion for (c)
The current is less than the 2.00 A that flowed through \(R_{2}\) when it was connected in parallel to the battery in the previous parallel circuit example.
Strategy and Solution for (d)
The power dissipated by \(R_{2}\) is given by
\(P_{2} = (I_{2})^2R_{2} = (1.61 \thinspace \mathrm{A})^2 (6.00 \thinspace \Omega) = 15.5 \thinspace \mathrm{W}.\)
Discussion for (d)
The power is less than the 24.0 W this resistor dissipated when connected in parallel to the 12.0-V source.
APPLYING THE SCIENCE PRACTICES: CIRCUIT CONSTRUCTION KIT (DC ONLY)
Plan an experiment to analyze the effect on currents and potential differences due to rearrangement of resistors and variations in voltage sources. Your experimental investigation should include data collection for at least five different scenarios of rearranged resistors (i.e., several combinations of series and parallel) and three scenarios of different voltage sources.
PRACTICAL IMPLICATIONS
One implication of this last example is that resistance in wires reduces the current and power delivered to a resistor. If wire resistance is relatively large, as in a worn (or a very long) extension cord, then this loss can be significant. If a large current is drawn, the \(IR\) drop in the wires can also be significant.
For example, when you are rummaging in the refrigerator and the motor comes on, the refrigerator light dims momentarily. Similarly, you can see the passenger compartment light dim when you start the engine of your car (although this may be due to resistance inside the battery itself).
What is happening in these high-current situations is illustrated in Figure 6. The device represented by \(R_3\) has a very low resistance, and so when it is switched on, a large current flows. This increased current causes a larger \(IR\) drop in the wires represented by \(R_1\), reducing the voltage across the light bulb (which is \(R_2\)), which then dims noticeably.

Figure 6. Why do lights dim when a large appliance is switched on? The answer is that the large current the appliance motor draws causes a significant IR drop in the wires and reduces the voltage across the light.
PROBLEM-SOLVING STRATEGIES FOR SERIES AND PARALLEL RESISTORS
- Draw a clear circuit diagram, labeling all resistors and voltage sources. This step includes a list of the knowns for the problem, since they are labeled in your circuit diagram.
- Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful.
- Determine whether resistors are in series, parallel, or a combination of both series and parallel. Examine the circuit diagram to make this assessment. Resistors are in series if the same current must pass sequentially through them.
- Use the appropriate list of major features for series or parallel connections to solve for the unknowns. There is one list for series and another for parallel. If your problem has a combination of series and parallel, reduce it in steps by considering individual groups of series or parallel connections, as done in this module and the examples. Special note: When finding \(R_p\), the reciprocal must be taken with care.
- Check to see whether the answers are reasonable and consistent. Units and numerical results must be reasonable. Total series resistance should be greater, whereas total parallel resistance should be smaller, for example. Power should be greater for the same devices in parallel compared with series, and so on.